斜率截距公式
斜率截距公式是表示直线的最简单、��最常用的方法!学会了它,你就能轻松画出任何直线了。
什么是斜率截距公式?
斜率截距公式是表示一次函数(直线)的标准形式:
y = mx + b
其中:
- y:因变量(函数值)
- x:自变量
- m:斜率(slope),表示直线的倾斜程度
- b:y 轴截距(y-intercept),表示直线与 y 轴的交点
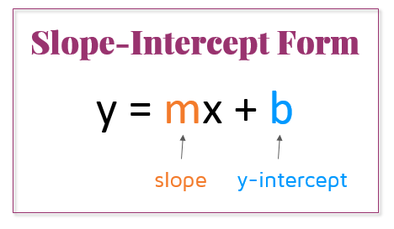
公式的组成部分
斜率(m)
斜率表示直线的倾斜程度:
- m > 0:直线向右上方倾斜(正斜率)
- m < 0:直线向右下方倾斜(负斜率)
- m = 0:直线是水平的(平行于 x 轴)
- |m| 越大:直线越陡峭
y 轴截距(b)
y 轴截距是直线与 y 轴交点的纵坐标:
- 当 x = 0 时,y = b
- 所以点 (0, b) 在直线上
如何求斜率?
方法 1:从两点求斜率
如果知道直线上两点 (x₁, y₁) 和 (x₂, y₂):
斜率 m = (y₂ - y₁) / (x₂ - x₁)
例子:
- 点 A(1, 3) 和点 B(3, 7)
- 斜率 m = (7 - 3) / (3 - 1) = 4 / 2 = 2
方法 2:从公式中直接看
如果已经知道公式 y = mx + b,m 就是斜率:
y = 3x + 2
↑
斜率 m = 3
如何求 y 轴截距?
方法 1:从公式中直接看
如果已经知道公式 y = mx + b,b 就是 y 轴截距:
y = 3x + 2
↑
y 轴截距 b = 2
方法 2:代入 x = 0
在公式中,令 x = 0:
y = 3x + 2
y = 3×0 + 2
y = 2
所以 y 轴截距是 2,直线经过点 (0, 2)。
实际例子
例子 1:y = 3x + 2
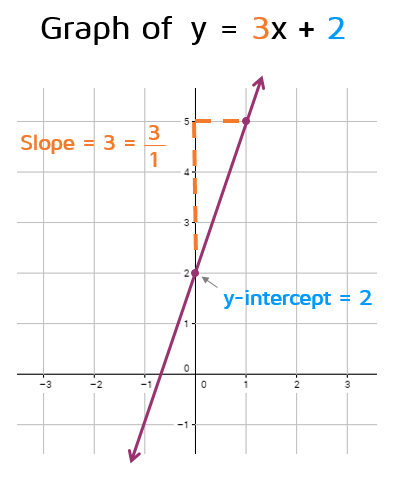
- 斜率 m = 3:直线向右上方倾斜,每向右移动 1 个单位,向上移动 3 个单位
- y 轴截距 b = 2:直线与 y 轴交于点 (0, 2)
例子 2:y = (1/4)x + 1
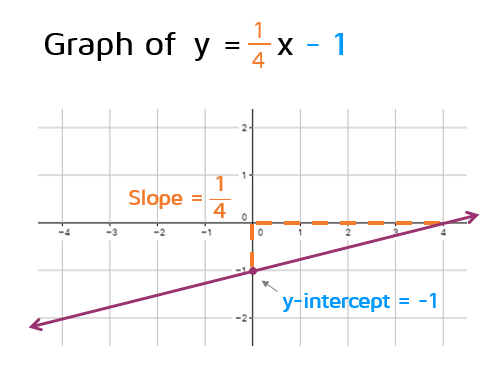
- 斜率 m = 1/4:直线向右上方倾斜,但比较平缓
- y 轴截距 b = 1:直线与 y 轴交于点 (0, 1)
如何画直线?
步骤
- 找到 y 轴截距:在 y 轴上标出点 (0, b)
- 利用斜率:从 (0, b) 开始,按照斜率 m 移动
- 如果 m = 3,向右 1 个单位,向上 3 个单位
- 如果 m = -2,向右 1 个单位,向下 2 个单位
- 连接两点:画一条直线通过这两点
例子:�画 y = 2x + 1
- y 轴截距 b = 1,标出点 (0, 1)
- 斜率 m = 2,从 (0, 1) 向右 1 个单位,向上 2 个单位,得到点 (1, 3)
- 连接 (0, 1) 和 (1, 3),延长得到直线
生活中的应用
速度问题
- 🚗 汽车以 60 公里/小时的速度行驶
- 公式:距离 = 60 × 时间
- 用 y = mx + b 表示:y = 60x(b = 0,从起点开始)
费用问题
- 💰 打车起步价 10 元,每公里 2 元
- 公式:费用 = 2 × 公里数 + 10
- 用 y = mx + b 表示:y = 2x + 10
- 斜率 m = 2(每公里 2 元)
- 截距 b = 10(起步价)
温度转换
- 🌡️ 摄氏度转华氏度:F = (9/5)C + 32
- 斜率 m = 9/5
- 截距 b = 32
特殊情况的斜率截距公式
水平线
y = b
- 斜率 m = 0
- 所有点的 y 坐标都是 b
- 例子:y = 5(一条水平线)
垂直线
x = a
- 斜率不存在(无穷大)
- 不能用 y = mx + b 表示
- 所有点的 x 坐标都是 a
- 例子:x = 3(一条垂直线)
经过原点的直线
y = mx
- y 轴截距 b = 0
- 直线经过原点 (0, 0)
- 例子:y = 2x
从标准形式转换为斜率截距公式
标准形式:Ax + By = C
转换步骤:
- 把含 y 的项移到一边
- 把 y 的系数化为 1
例子:
2x + 3y = 6
3y = -2x + 6 (移项)
y = (-2/3)x + 2 (除以 3)
所以斜率 m = -2/3,y 轴截距 b = 2。
小练习
- 在 y = 3x + 2 中,斜率和 y 轴截距分别是多少?
- 如果直线经过点 (0, 5) 和 (2, 9),求斜率截距公式
- 画直线:y = 2x - 1
- 把 3x + 2y = 6 转换为斜率截距形式
- 应用题:打车起步价 8 元,每公里 3 元,写出费用公式
💡 小贴士:记住"y = mx + b",m 是斜率(倾斜程度),b 是 y 轴截距(与 y 轴的交点)。掌握了这个公式,你就能轻松处理所有直线问题!