跳到主要内容

PCL 点云矩阵变换（RT 矩阵）

在 3D 点云处理中，RT 矩阵是一个常用的工具，用于对点云进行旋转和平移操作。本文将详细介绍 RT 矩阵的概念，并通过一个示例程序演示如何基于 PCL 和 Eigen 库将一帧点云进行矩阵变换再输出。

提示

本教程的示例代码和点云数据可在 GitHub 下载。

RT 矩阵​

RT 矩阵包含旋转矩阵（R）和平移向量（T），组合起来可以描述一个刚体变换。具体来说，RT 矩阵是一个 4x4 的同质坐标变换矩阵，包含两个部分：

  1. 旋转矩阵（R）：这是一个 3x3 的矩阵，用于描述点云的旋转。旋转矩阵是一个正交矩阵，表示绕某个轴的旋转。
  2. 平移向量（T）：这是一个 3x1 的向量，用于描述点云的平移。平移向量表示在各个方向上的移动距离。

组合起来，RT 矩阵可以表示为：

           |-------> This column is the translation
    | 1 0 0 x |  \
    | 0 1 0 y |   }-> The identity 3x3 matrix (no rotation) on the left
    | 0 0 1 z |  /
    | 0 0 0 1 |    -> We do not use this line (and it has to stay 0,0,0,1)

其中，R 是 3x3 的旋转矩阵，T 是 3x1 的平移向量，右下角的 1 是为了使矩阵成为同质坐标形式的 4x4 矩阵。

旋转矩阵（R）​

旋转矩阵通常可以通过欧拉角、旋转向量或四元数来计算。

欧拉角：通过绕固定轴（如 X, Y, Z 轴）依次旋转相应的角度来构建旋转矩阵。例如：

  • 绕 X 轴旋转角度（α\alpha）

    Rx(α)=[1000cos⁡α−sin⁡α0sin⁡αcos⁡α]\mathbf{R_x}(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix}

  • 绕 Y 轴旋转角度（β\beta）

    Ry(β)=[cos⁡β0sin⁡β010−sin⁡β0cos⁡β]\mathbf{R_y}(\beta) = \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix}

  • 绕 Z 轴旋转角度（γ\gamma）

    Rz(γ)=[cos⁡γ−sin⁡γ0sin⁡γcos⁡γ0001]\mathbf{R_z}(\gamma) = \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix}

通过将这些旋转矩阵按顺序相乘，可以得到最终的旋转矩阵 R\mathbf{R}。

旋转向量：通过旋转轴和旋转角度来构建旋转矩阵。旋转向量表示绕一个单位向量旋转一定角度，使用 Rodrigues 公式可以将其转换为旋转矩阵。

四元数：四元数是一种表示旋转的方式，能够避免欧拉角的万向节锁问题。通过四元数转换公式可以得到旋转矩阵。

平移向量（T）​

平移向量是一个简单的 3x1 向量，表示在 X, Y, Z 三个方向上的平移量：

T=[txtytz]\mathbf{T} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}

应用 RT 矩阵进行点云变换​

假设有一个 3D 点 P=[xyz]T\mathbf{P} = \begin{bmatrix} x & y & z \end{bmatrix}^T，其同质坐标表示为 Ph=[xyz1]T\mathbf{P_h} = \begin{bmatrix} x & y & z & 1 \end{bmatrix}^T。

应用 RT 矩阵进行变换可以表示为：Ph′=RT⋅Ph\mathbf{P'_h} = \mathbf{RT} \cdot \mathbf{P_h} 。

其中，Ph′=[x′y′z′1]T\mathbf{P'_h} = \begin{bmatrix} x' & y' & z' & 1 \end{bmatrix}^T，展开后为：

[x′y′z′1]=[R11R12R13txR21R22R23tyR31R32R33tz0001]⋅[xyz1]\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

经过计算，变换后的点 P′\mathbf{P'} 的坐标为：

P′=[x′y′z′]=R⋅[xyz]+T\mathbf{P'} = \begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} = \mathbf{R} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} + \mathbf{T}

通过 RT 矩阵的应用，可以对一整帧点云的每一个点进行旋转和平移，从而实现点云的刚体变换。

示例程序​

下面使用 PCL 库（Point Cloud Library）来实现将一帧点云经过 RT 矩阵转换输出另一帧点云，并将两帧点云同时可视化进行对比的演示。完整示例代码如下所示。

transform_demo.cpp
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/common/transforms.h>
#include <Eigen/Dense>
#include <thread>
#include <chrono>

int main(int argc, char** argv)
{
    // 检查命令行参数
    if (argc != 2) {
        PCL_ERROR("Usage: %s <input.pcd>\n", argv[0]);
        return -1;
    }

    // 创建点云对象并读取PCD文件
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
    if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) == -1) {
        PCL_ERROR("Couldn't read the file %s\n", argv[1]);
        return -1;
    }

    // 创建RT矩阵，将矩阵初始化为单位矩阵
    Eigen::Matrix4f transform = Eigen::Matrix4f::Identity();

    // 定义旋转矩阵 (绕Z轴旋转45度)
    float theta = M_PI / 4; // 弧度制角度
    transform(0, 0) = cos(theta);
    transform(0, 1) = -sin(theta);
    transform(1, 0) = sin(theta);
    transform(1, 1) = cos(theta);

    // 定义平移向量 (平移 x 方向2.5米, y 方向0米, z 方向1米)
    transform(0, 3) = 2.5;
    transform(1, 3) = 0.0;
    transform(2, 3) = 1.0;

    // 创建变换后的点云
    pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_cloud(new pcl::PointCloud<pcl::PointXYZ>);
    pcl::transformPointCloud(*cloud, *transformed_cloud, transform);

    // 创建可视化对象
    pcl::visualization::PCLVisualizer::Ptr viewer(new pcl::visualization::PCLVisualizer("3D Viewer"));
    viewer->setBackgroundColor(0, 0, 0);

    // 设置原始点云的颜色为白色
    pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> original_color(cloud, 255, 255, 255);
    viewer->addPointCloud<pcl::PointXYZ>(cloud, original_color, "original cloud");

    // 设置变换后点云的颜色为红色
    pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> transformed_color(transformed_cloud, 255, 0, 0);
    viewer->addPointCloud<pcl::PointXYZ>(transformed_cloud, transformed_color, "transformed cloud");

    // 设置点云大小
    viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "original cloud");
    viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "transformed cloud");

    // 添加坐标系
    viewer->addCoordinateSystem(1.0);
    viewer->initCameraParameters();

    // 开始可视化
    while (!viewer->wasStopped()) {
        viewer->spinOnce(100);
        std::this_thread::sleep_for(std::chrono::milliseconds(100));
    }

    return 0;
}

改程序依赖 PCL 库和 VTK 库，配套 CMakeLists.txt 文件如下：

CMakeLists.txt
cmake_minimum_required(VERSION 3.1)
project(transform_demo)

find_package(PCL REQUIRED)
find_package(VTK REQUIRED)

include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})

add_executable(${PROJECT_NAME} transform_demo.cpp)
target_link_libraries(${PROJECT_NAME} ${PCL_LIBRARIES} ${VTK_LIBRARIES})

依次执行以下命令编译源代码：

$ mkdir build && cd build
$ cmake ..
$ make

编译完成后，执行 transform_demo 演示程序，指定 PCD 文件：

$ ./transform_demo ../data/2024-04-09-22-06-07.pcd

输出结果如下：

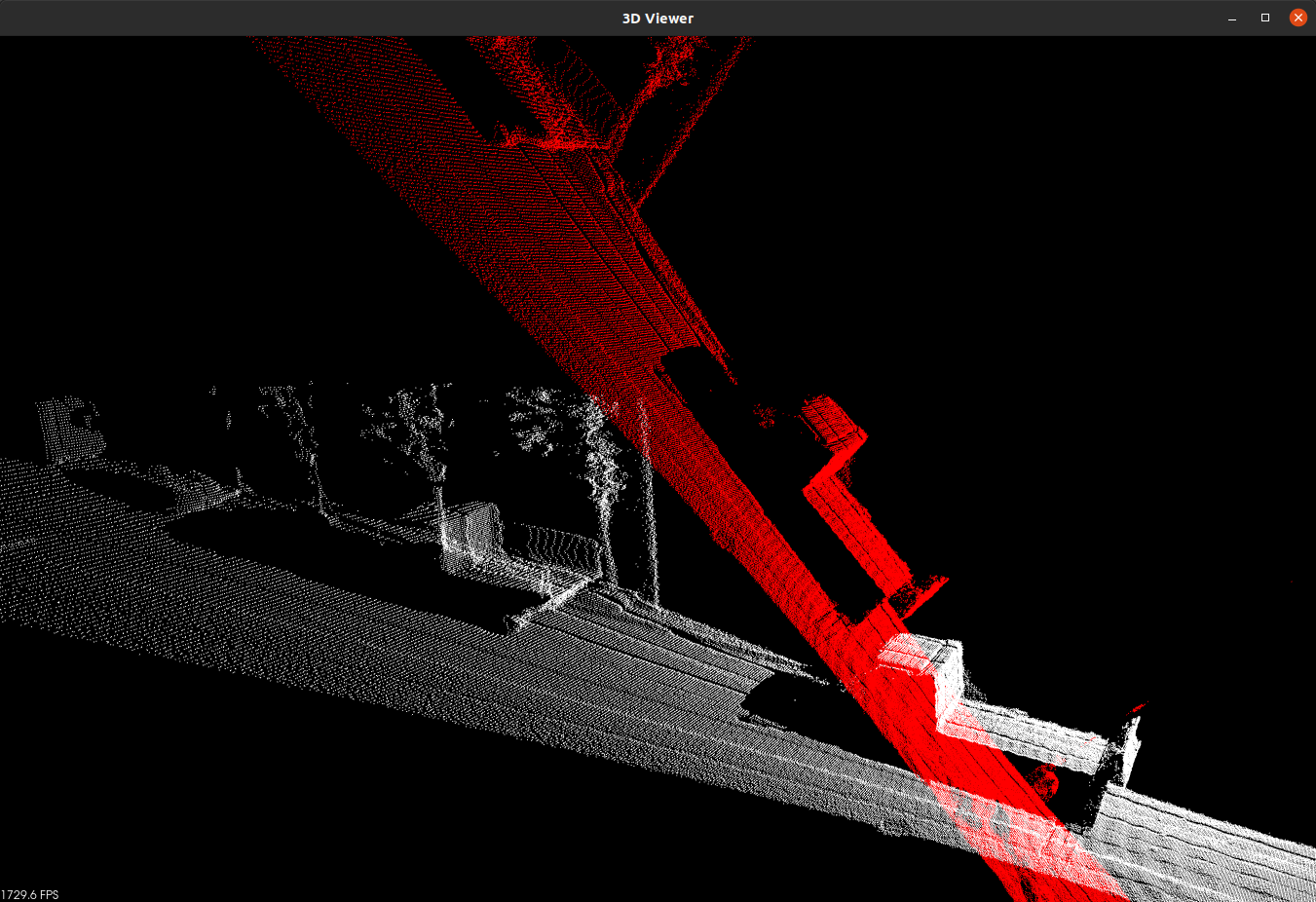
可以看到白色为原始点云，红色为经过旋转、平移后的点云。

小结​

矩阵变换是点云处理中的一个重要的工具，本文介绍了 RT 矩阵的基本概念和计算方法，RT 矩阵可用于对 3D 点云进行旋转和平移操作。我们通过一个例子演示了如何通过 PCL 和 Eigen 构建 RT 矩阵并实现 3D 点云的旋转平移，相信你已经掌握点云的矩阵变换操作啦！